Interés: clases, funcionamiento y fórmulas.
1. Clases de interés
El interés es el lucro, retribución o renta o ganancia producido por un capital.
Se clasifican los intereses según diversos criterios que a veces se superponen. Además, los criterios clasificatorios en ciertos casos tienen que ver con conceptos que hacen a la procedencia y en otros con tasas o sus modos de cálculo.
Y, transcurrido siglo y medio aproximadamente desde las codificaciones comercial y civil, son todavía imprecisas las denominaciones indicativas de las distintas funciones del interés y se hace equívoca su aplicación.
2. Interés simple y compuesto
a) Interés simple
En el interés simple, el capital no muda y siempre se aplica la tasa sobre el capital inicial.
El interés simple es el de un capital sin agregarle ningún rédito vencido, aun cuando no se haya cobrado. Se dice que un capital produce interés simple cuando éste es directamente proporcional al capital inicial y al tiempo de duración de la operación [4].
La fórmula que permite resolver cualquier ecuación de interés simple, según se vayan colocando las incógnitas de cada uno de los elementos, es la siguiente: 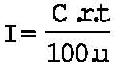
Los componentes de la fórmula son:
I: interés.
C: capital.
r: razón o tanto por ciento, generalmente anual.
t: tiempo, generalmente expresado en años o fracciones de año.
u: fracciones en que se divide la unidad de tiempo.
Ejemplo:
Averiguar el interés que produce un capital de 300 unidades monetarias, al 12% anual, colocado durante un período de seis meses.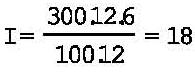
Ello, sumado al capital originario, da 318 unidades monetarias.
b) Interés compuesto
En el interés compuesto se reúnen periódicamente los intereses al capital, y la tasa se aplica en el próximo período sobre el nuevo capital. El período que se toma en cuenta para acumular los intereses al capital se 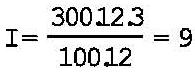
Ello, sumado al capital originario, da 309 unidades monetarias.llama "período de capitalización". El interés compuesto es el de un capital al que van acumulándose los réditos para que produzcan otros, por lo cual se habla de tasa acumulada.
Ejemplo:
El mismo capital de 300 unidades monetarias, colocado a interés compuesto, con capitalización trimestral, da un total de 318,27 según el siguiente cálculo:
Tal cantidad, sumada a la vez al capital originario, da el total de 318,27 unidades monetarias.
Esto significa un interés simple del 12,18% anual, según el siguiente detalle: Está pagando 18,27 unidades de interés (9 + 9,27) por 300 unidades de capital. La tasa real se obtiene dividiendo lo pagado por lo prestado, en el caso: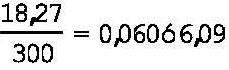
Como este dinero lo pagó por seis meses, la tasa anual se obtiene dividiéndola por 6 y multiplicándola por 12, con lo que se obtiene 12,18%.
En realidad, se hace el cálculo con la misma fórmula de interés simple, despejando la incógnita r.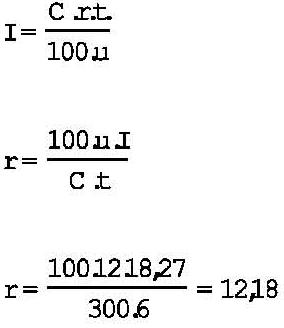
El mismo capital de 300 unidades monetarias, colocado a un interés compuesto, con capitalización bimestral en lugar de trimestral, da un total de 318,36, según el siguiente detalle: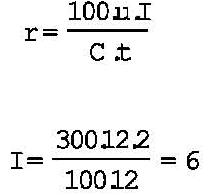
Ello, sumado al capital originario, da 306 unidades monetarias.
Tal cantidad, sumada a su vez al capital originario, da 312,12 unidades monetarias: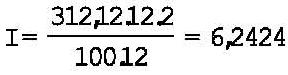
La nueva cantidad, sumada al capital originario, da un total de 318,36 unidades monetarias.
Esto significa un interés simple del 12,24%, anual, según el siguiente detalle: Está pagando 18,36 unidades de interés (6 + 6,12 + 6,24) por 300 unidades de capital. La tasa real se obtiene dividiendo lo pagado por lo prestado, en el caso:
Como este dinero lo pagó por 6 meses, la tasa anual se obtiene dividiéndola por 6 y multiplicándola por 12, con lo que se obtiene 12,24%. Volvamos a controlar el cálculo con la misma fórmula de interés simple, despejando la incógnita r.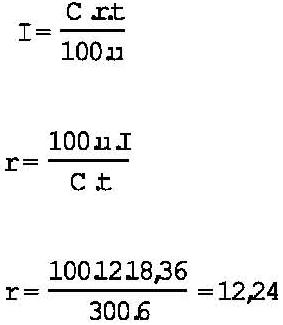
Y así sucesivamente; si la capitalización es mensual, la cantidad total que resultará será la de 318,45 unidades, con lo que la tasa real será de 12,30%.
La fórmula que permite resolver cualquier ecuación de interés compuesto sin necesidad de ir calculando los diversos intereses simples para sumarlos, según se vayan colocando las incógnitas de cada uno de los elementos, es la siguiente: 
Los componentes de la fórmula son:
A: capital más sus intereses (es decir C+I).
C: capital.
r: razón o tanto por ciento, generalmente anual.
n: tiempo generalmente expresado en años o fracciones de año, pero como es una potencia, se refiere a las veces en que se renueva la inversión.
Ejemplo:
El mismo capital de 300 unidades monetarias, colocado a interés compuesto, con capitalización trimestral, da un total de 318,27 unidades monetarias, según el siguiente detalle:
En la fórmula, donde dice r, en realidad primero hay que resolver: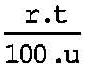
Ello, por cuanto la fórmula: 
se basa en la fórmula original de interés simple, quedando afuera:
debiéndonos atener a los restantes componentes: r, t, y u.
Se trata de una tasa de interés simple expresada en fracciones distintas al año: 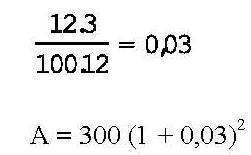
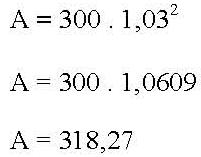
- En los restantes ejemplos, tendríamos: 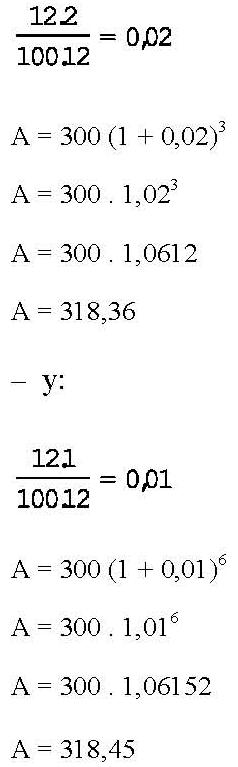
Al respecto, se ha decidido a nivel plenario que además de los supuestos establecidos en el texto legal positivo, existen otros en los que cabe la capitalización del interés devengado por un crédito cuyo obligado se encuentre en mora . En consecuencia, quedó establecido que la referencia a las tasas que emplea el Banco de la Nación no se limita al monto de los intereses, sino que comprende también la modalidad con que el cálculo se realiza, ya que de lo contrario quedaría desvirtuada la sustancia del sistema, entendiéndose que cuando el magistrado se remite a tasas de corto plazo, será fatal la liquidación del fruto con su capitalización, con la secuencia temporal utilizada por la entidad bancaria al emplear esa tasa en sus operaciones corrientes, y que esto no es, económicamente, la capitalización del artículo 623 del Código Civil sino que constituye simplemente la recepción en justicia de los efectos implícitos desde el primer momento en la concurrente aplicación de los artículos 632 del Código Civil y 565 del Código de Comercio .
La reforma legal al artículo 623 del Código Civil en cuanto al anatocismo es de relevancia, pues antes decía "no se deben intereses de los intereses sino por obligación posterior, convenida entre deudor y acreedor, que autorice la acumulación de ellos al capital..." y ahora admite que "no se deben intereses de los intereses, sino por convención expresa que autorice su acumulación al capital con la periodicidad que acuerden las partes..." Ello dio lugar a que se dijera que hasta la palabra anatocismo es vieja . También a que se atacara la reforma por insuficiente, dado que sólo corre la capitalización cuando existe convención de acumulación de los intereses al capital, dejando en desventaja a quien no lo pactó .
De ahí que no puede considerarse que la capitalización de intereses admitida de por sí conlleve una consecuencia patrimonial inaceptable para los deudores, y que si bien la obligación no puede superar ciertos extremos, los deudores a estos fines deben practicar una cuenta alternativa a fin de demostrar en forma concreta el perjuicio que les causa el modo de liquidar la deuda . Es que, dado que el artículo 623 del Código Civil luego de la reforma impuesta por la ley 23.928, autoriza la capitalización de intereses cuando éstos han sido pactados, cabe considerar que tal convención no puede ser dejada de lado por los jueces, so pena de caer en la arbitrariedad, salvo que la misma comprometa el orden público o las buenas costumbres. Por ende, se requieren fundados motivos para resolver de manera distinta a la pactada.
No obstante, hay que tener cuidado con los límites a la capitalización, dado que el mecanismo -en forma disimulada pues las tasas no impresionan de por sí- puede llevar a cifras exorbitantes. De tal modo, no cabe la capitalización si en el caso particular conlleva una consecuencia patrimonial inadmisible para el deudor que trascienda el límite de la moral y las buenas costumbres . Ello es especialmente predicable de la tasa de capitalización diaria, que se ha dado en llamar "capitalización continua". Se apunta que el interés continuo se da cuando la capitalización se hace continuamente y sin que medien períodos finitos entre una capitalización y otra. La diferencia entre el interés compuesto y el interés continuo se hace más apreciable cuanto mayor es el tiempo de la capitalización, ya que en el interés continuo la capitalización es permanente. Las planillas computadorizadas que la generalidad de los bancos presentan a juicio reflejan tasas que permanecen estables durante varios períodos de tiempo y parecen tasas normales en sus respectivas fechas. Pero lo que no permanece estable es el capital, en una formulación matemática que da lugar a enormes y exorbitantes diferencias .
Sobre el punto, un tribunal ha dicho que la capitalización de intereses es procedente; mas la capitalización diaria es tanto como admitir que el banco, a lo largo de los años, cada día ha obtenido un cliente dispuesto a pagar los altísimos intereses que se han aplicado, y ello sin gasto alguno administrativo, ya que no hay empleados a quienes pagar, contabilidades que llevar, ni papelería que llenar (todo es pura ganancia); que la aplicación de intereses con capitalización diaria resulta lesiva a los artículos 953 y 1071 del Código Civil y obliga a disponer su morigeración sobre la base de que los mismos no superen, en conjunto, el resultado que se obtendría de actualizar el capital originario al 31 de marzo de 1991 y sumar a ello los importes resultantes de liquidar sobre tal capital intereses a una tasa del 18% anual a partir del 1° de abril de 1991, y que, con referencia al importe sumado de capital e intereses obtenido, se liquidarán intereses con la ya aludida tasa del 18% anual .
La propia Corte Suprema de Justicia de la Nación entendió que los agravios suscitan cuestión federal para su consideración en la vía extraordinaria cuando cabe invalidar lo resuelto con menoscabo de los derechos de propiedad y de defensa en juicio, al haberse apartado el tribunal de la realidad económica del caso y haber desatendido las consecuencias patrimoniales de su fallo, si la sentencia -por remisión al fallo plenario dictado en la causa "Uzal c/Moreno"- convalida la capitalización permanente y en breves lapsos y lleva una consecuencia patrimonial equivalente a un despojo del deudor, cuya obligación no puede exceder el crédito actualizado con un interés que no trascienda los límites de la moral y buenas costumbres .

Comentarios
Publicar un comentario